量子化制御
一般に動的システムの制御においては,制御対象への入力が連続値であることを前提として制御器(たとえばPID制御器)を設計します.しかし,現実には,制御対象への入力が離散値に制限される場合もあります.たとえば,ON/OFFなどの離散値を出力するアクチュエータを用いる場合や,通信容量の制限されたディジタル通信路を利用する場合などです.このような離散値入力のシステムの制御は,従来の連続値入力のシステムの場合に比べると難しくなります(教科書レベルではなくなる).この問題に対して,われわれは,連続値を離散値に変換する量子化器を用いるアプローチに注目しています.具体的には,量子化器を制御対象の前段に直列結合したシステムの入出力特性を連続値システム(理想的なシステム)の入出力特性に最も近くする動的な量子化器の設計問題を考えています.このような最適動的量子化器が得られれば,離散値入力システムの設計において,これまでに整備されてきた連続値入力システムに対する線形制御理論を適用でき,離散値入力システムの設計が容易になることが期待できます.
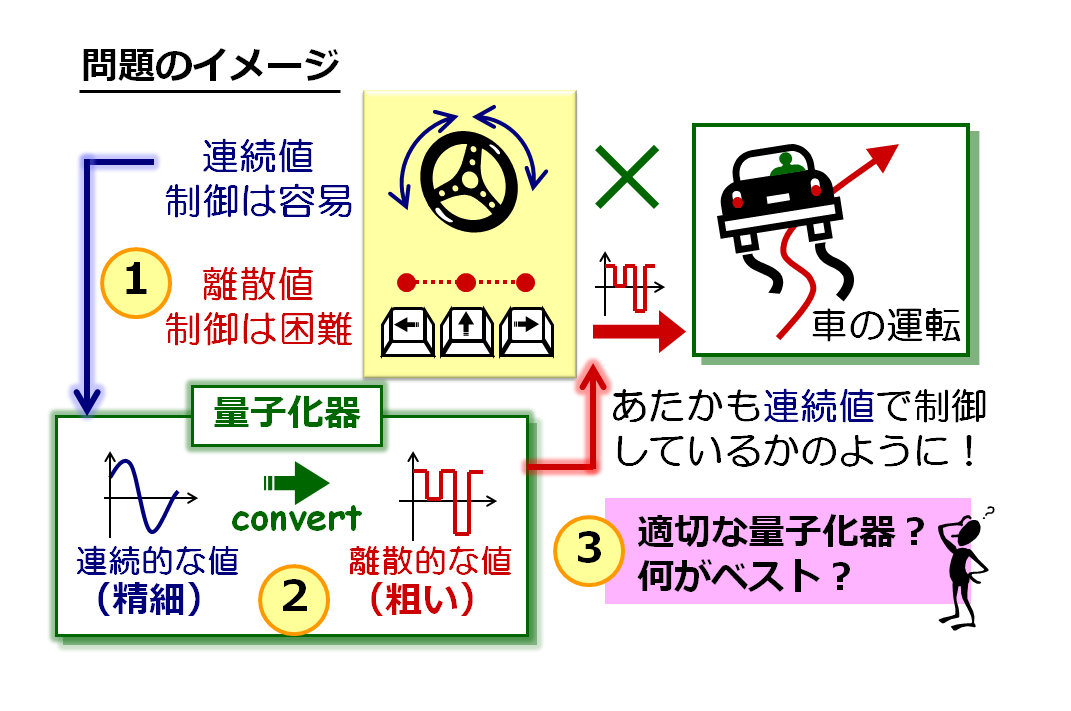
上の図は,量子化器の設計問題のイメージです.車の運転を想像してください.ハンドルで連続的に進む方向を変える状況であれば,運転はそれほど難しくないでしょう.しかし,三つのボタンで進む方向を離散的に変える状況になれば,一気に運転が難しくなります.つまり,連続情報より離散情報を利用することで制御が難しくなるということです.これに対して,本研究では,あたかもハンドル(連続情報)で運転しているかのような結果が得られる離散情報を「量子化器」で生成することを考えます.これにより,離散情報しか利用できない場合でも,ハンドルで運転することができます(従来の良く知っている運転技術が利用可能).ただし,適切な量子化器をもってこないといけませんので,「何が最適か?」を考えることが本研究の目的となっています.
最適動的量子化器
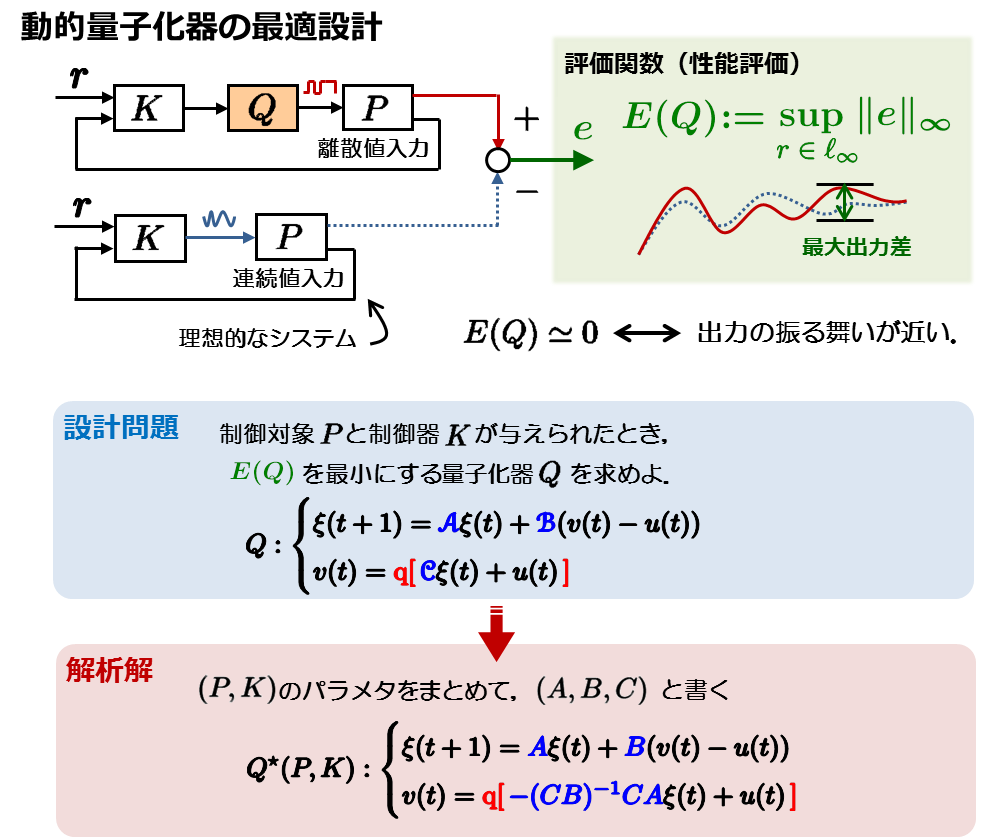
離散値入力システムと連続値入力システムの出力差をl∞ノルムで評価し,動的量子化器の設計問題を定式化しています.そして,その問題の最適解を解析的に(代数的な計算で)導出しています.この最適な動的量子化器は,与えられた制御対象と制御器のパラメータで特徴づけられています.なお,下図のフィードバック系に限らず,より一般的なシステム(線形システムと量子化器のフィードバック結合系)に対して,解が得られていますので,フィードフォワード系などに対しても最適動的量子化器を与えることができます.
機械システム制御への応用
機械システムの離散値制御をとおして,動的量子化器の有用性を検証しています.
| シーソーカート系 | ||
| 連続値入力(理想) | 離散値入力(動的量子化) | 離散値入力(静的量子化) |
| シーソーカート系 | ||
| 連続値入出力(理想) | 離散値入出力(動的量子化) | 離散値入出力(静的量子化) |
| 回転型倒立振子系 | ||
| 連続値入力(理想) | 離散値入力(動的量子化) | 離散値入力(静的量子化) |
分散型動的量子化器の設計,マルチレート動的量子化器の設計
制御対象と制御器を物理的に分離しネットワーク通信路で結ぶ場合,制御対象の入力側と出力側にそれぞれ量子化器を配置する必要があります.そのような設定においては,分散型の量子化器を設計しなければなりません.この分散型量子化器の設計に対しても,ひとつの答えを与えています.
また,ハードウェアの制約から,制御対象の入力側と出力側でサンプリング周期が異なる場合があります.このようなマルチレート系における動的量子化器の設計にも取り組んでいます。
n次元システムのための動的量子化器と画像処理への応用
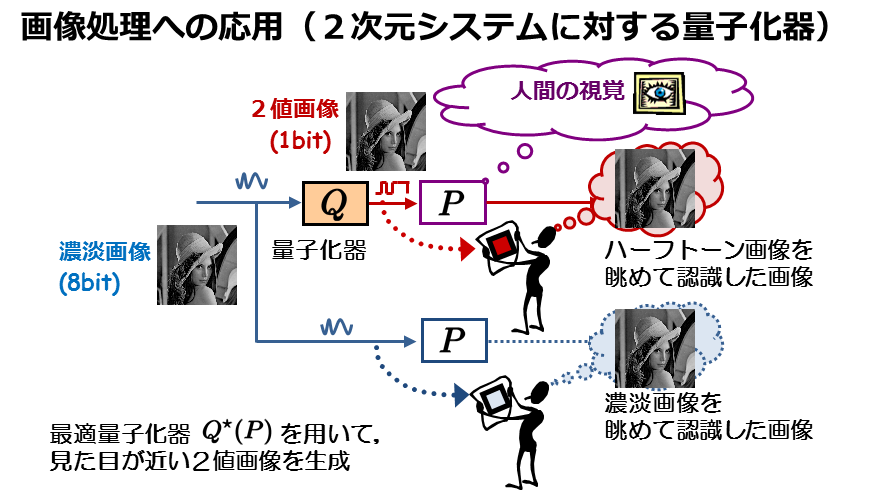
独立変数がn個あるシステムに対して,最適な量子化器を与えています.また,2次元システムのための最適量子化器を画像処理(ハーフトーン処理)に応用しました.ハーフトーン処理は2値化処理手法の一つで,白と黒の点の密度を変化させることで,濃淡画像に見た目が似ている2値画像を生成します.我々は,人間の視覚特性を考慮したハーフトーン処理アルゴリズムを量子化器の考え方を利用して構築しました.具体的には,濃淡画像を人間の目で見て認識した画像,そしてハーフトーン画像を目で見て認識した画像の二つが近くなるように,量子化器を構成しています.
CADツールの開発
Matlab上で,量子化器の解析・設計・評価を行うためのツールボックス(ODQtoolbox,ODQLab)を開発しています.詳しくはこちら(外部ページ).
現在取り組んでいるテーマ(システムの直列分解に基づくアプローチ)
これまでの量子化器の設計手法では,非最小位相形に対する設計や,固定次数の設計が代数的な計算ではできませんでした(数値最適化手法を援用すれば可能).この問題を解決するために,システムを二つのサブシステムに直列分解し,片方のサブシステムの情報を用いて,量子化器を構成する手法を考えています.直列分解方法を理論的に考察することが課題として残されていますが,量子化器設計のファイナルアンサーに近づいたといえます.